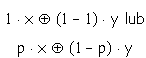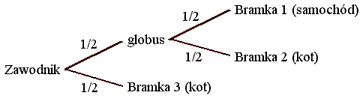| |
|
WYBÓR
W WARUNKACH NIEPEWNOŚCI
Do tej pory, badając zachowanie konsumenta na rynku, zakładaliśmy,
że:
- Istnieje pełna informacja (ceny, stopy procentowe, inflacja, itp.)
- Istnieje pewny wybór między alternatywami (zawsze zostanie wybrana
któraś z dostępnych możliwości)
Jednak sytuacja całkowitej pewności wszystkiego jest niemożliwa. Dlatego
w celu urzeczywistnienia rozważań mikroekonomicznych uchylamy założenie
o pewnym wyborze między alternatywnymi wariantami.
W rzeczywistości znamy dostępne alternatywy oraz prawdopodobieństwo
wyboru zaistnienia z nich. Dobrym modelem opisującym tę sytuację jest
teleturniej "Idź na całość".
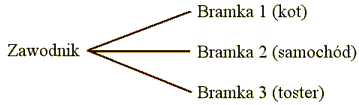
Prawdopodobieństwo wyboru każdej z bramek
wynosi 1/3. Homo Economicus wstępując do programu "Idź na całość"
wkracza w świat niepewności. Musi on podejmować ryzykowne wybory.
Loteria
Loterię określamy w następujący sposób
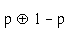
p - prawdopodobieństwo, że zajdzie sytuacja x
1-p - prawdopodobieństwo, że zajdzie sytuacja y.
Znak 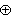 oznacza,
że sytuacje x i y wykluczają się. oznacza,
że sytuacje x i y wykluczają się.
Sytuacja, w której zachodzi
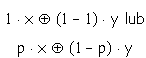
oznacza, że wybór sytuacji x jest pewny.
Jeśli mamy dwie loterie, to sytuacja wygląda następująco
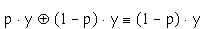
Kolejność nie ma wpływu na postrzeganie loterii. Obie loterie są
jednakowo traktowane.
(W tym miejscu powinien być kolejny, tym razem bardziej makabryczny,
wzór, ale ja nie miałem notatek, więc nie wiem jak go zapisać)
Oznacza to znów, że dwie loterie są takie same. Jednak w tej sytuacji
można zredukować loterię. Na przykład
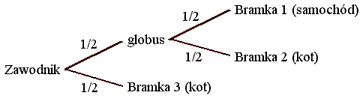
Tym razem gra jest dwuetapowa. W pierwszym etapie zawodnik wybiera
pomiędzy globusem a bramką 1 z tym samym prawdopodobieństwem równym
1/2. Jeśli wybierzemy globus, to w drugim etapie możemy wybierać
pomiędzy bramką 1 (samochód) a bramką 2 (znowu kot). Zatem prawdopodobieństwo
wybrania samochodu wynosi 1 (1/2 * 1), natomiast prawdopodobieństwo
wylosowania kota wynosi 1 (1/2 + 1).
Każda z opisanych sytuacji jest loterią. Konsument musi teraz wybierać
między loteriami. W przypadku większej liczby loterii można zastosować
aksjomaty racjonalnego wyboru.
Kompletność
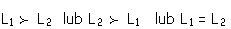
Przechodniość
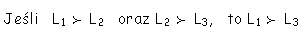
Każda loteria jest tak samo dobra
L1 = L1
Szukamy teraz funkcji użyteczności odpowiadającej preferencjom konsumenta
dokonującego wyboru w warunkach niepewności. Np.
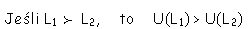
Po rozpisaniu
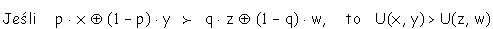
Jednak nie zawsze kryterium wartości oczekiwanej jest dobre. Von
Neumann i Morgenstern stwierdzili, że można łączyć tylko te funkcje
użyteczności, co do których mamy pewność wyboru. W warunkach pewności
zawodnik zawsze wybierze grę, która ma dla niego większą użyteczność.
Natomiast jak wygląda funkcja użyteczności dla wyboru w warunkach niepewności.
Załóżmy, że uczestnik gry "Idź na całość" ma kapitał początkowy w wysokości
1000 zł. Staje on przed następującym wyborem.

Prawdopodobieństwo wyboru każdej z tych sytuacji
jest równe i wynosi 1. Zatem szansa wygranej (będzie miał 21000 zł) jest
taka sama jak szansa
przegranej (pozostanie mu początkowy 1000 zł). W tym przypadku zawodnik
waży swoją użyteczność prawdopodobieństwami zajścia każdej z sytuacji.
Zatem jego oczekiwana użyteczność będzie wynosiła
U = p * U(x1) + p * U(x2)
Geometrycznie wartość oczekiwana jest środkiem odcinka łączącego punkty
oznaczające każdą z sytuacji.
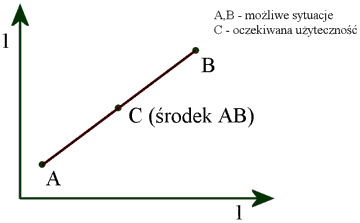
W przypadku, gdy sytuacje A i B zachodzą z różnymi prawdopodobieństwami,
punkt oczekiwanej użyteczności będzie w odpowiednich proporcjach dzielił
odcinek AB.
Definiujemy trzy rodzaje zawodników:
- Zawodnik 1 nie chce grać, czyli wybiera L2 (ma awersję do ryzyka).
Ten zawodnik woli użyteczność wartości oczekiwanej gry w stosunku
do użyteczności oczekiwanej gry (wartość 50000 zaproponowanych mu
w L2 jest dla niego większa niż udział w L1, która ma tę samą wartość
oczekiwaną).
- Zawodnik 2 jest osobą neutralną względem ryzyka. Dla niego udział
w grze (wybór L1) lub wybranie L2 oznacza to samo. Ocenia on grę według
wartości oczekiwanej. Dla niego wartość oczekiwana gry jest równa użyteczności
wartości oczekiwanej gry.
- Zawodnik 3 jest osobą skłonną do ryzyka. Wybierze on grę (L1). Użyteczność
oczekiwana gry jest dla niego większa od użyteczności wartości oczekiwanej
gry.
Osoba, która ma awersję do ryzyka mając do wyboru grę i sytuację pewną,
wybierze grę wówczas, gdy wartość oczekiwana tej gry będzie większa
od rekompensaty, jaką otrzymałby nie biorąc udziału w grze.
|
|
|
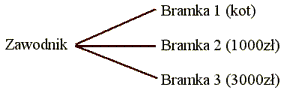
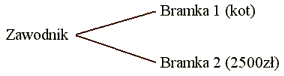
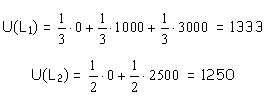
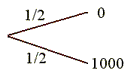
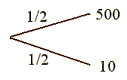
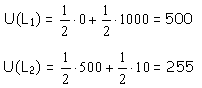
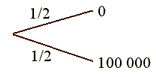 pewne
50000
pewne
50000