APLIKACJE WYBORU W WARUNKACH NIEPEWNOŚCI

ubezpieczenia
rynki finansowe

Ubezpieczenia
Gracz z przykładu 3 (poprzedni temat) może wybrać loterię L1 i z prawdopodobieństwem 0,5 wygrać 100000 zł lub wybrać L2 i z prawdopodobieństwem 1 wygrać 50000 zł.
W życiu konsumenci chcą zamieniać niepewność na sytuację pewną. Nie lubią żyć w świecie niepewności. Przykładem likwidacji niepewności są firmy ubezpieczeniowe. Zamieniają one za opłatą (polisa ubezpiecze-niowa) świat konsumenta z niepewnego w świat, w którym wszystko jest pewne.

Np.: Zakładamy, że z prawdopodobieństwem 0,1 Karol rozbije samochód o wartości 30000 zł, który stanowi jej cały majątek. Z prawdopodobieństwem 0,9 nic się nie stanie i nadal będzie on miał cały swój majątek. Ile Karol będzie skłonny zapłacić za ubezpieczenie ?
Składka ubezpieczeniowa zależy od funkcji użyteczności Karola.

1. Karol ma awersję do ryzyka. Funkcją jego użyteczności (U) względem bogactwa jest pierwiastek z wielkości bogactwa. Karol chce mieć taki sam poziom bogactwa niezależnie od tego, co się stanie. Wówczas funkcja użyteczności tej osoby ma postać
                                               
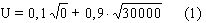
Teraz zakładamy, że ubezpieczenie jest pełne (firma ubezpieczeniowa odda nam to, co stracimy). Karol musi zapłacić składkę ubezpieczeniową (x). Wówczas funkcja użyteczności przyjmie postać
                                        
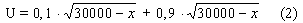
Po rozbiciu samochodu Karol otrzyma jego równowartość. Majątek Karola zostanie pomniejszony o wielkość składki ubezpieczeniowej (z prawdopodobieństwem 1 poziom bogactwa Karola będzie wynosił 30000 i x zł, niezależnie od tego, co się stanie - sytuacja pewna). Trzeba tylko obliczyć wysokość x.
Użyteczność w sytuacji, gdy się ubezpieczymy (2), musi być większa niż w sytuacji, gdy gramy (1). Czyli                                   
                                  
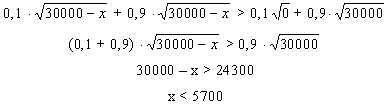
Składka musi być niższa od 5700 zł.
2. Zakładamy, że Leon jest neutralny względem ryzyka. Wycenia on wszystko według wartości oczekiwanej. W tym przypadku jego użyteczność jest równa wartości oczekiwanej gry, czyli ma postać:
                                                   U1 =0,1 0 + 0,9 30000
Natomiast, gdy się ubezpieczy, to
                                       U2 = 0,1 (30000 - x) + 0,9 (30000- x)
                                                             U1 = U2
Czyli x = 3000
3. Jacek jest ryzykantem. Jego funkcją użyteczności jest majątek podniesiony do kwadratu. Wówczas
                                     

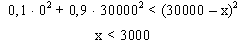
Jednak firma ubezpieczeniowa ubezpieczy tylko osobę mającą awersję do ryzyka, bo ubezpieczenie dwóch pozostałych osób jej się nie opłaca.

Rynki finansowe
Nasz Homo Oeconomicus jest graczem na giełdzie. Zakładamy, że ma on awersję do ryzyka. W loterii użyteczność Homo Oeconomicusa zależy od prawdopodobieństw zajścia danej sytuacji oraz od wielkości majątku, jaki chce on osiągnąć. Natomiast na giełdzie trudno jest operować prawdopodobieństwami. Trzeba poczynić trochę inne założenia.
                                          
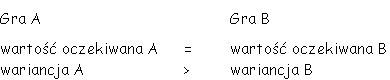
Osoba nie lubiąca ryzyka wybiera grę, która ma mniejszą wariancję przy tej samej wartości oczekiwanej.
Homo Oeconomicus grający na giełdzie zna notowania akcji, czyli ich ceny. Dodatkowo zna on wahania kursów akcji Bardzo Znanej Firmy z ostatniego roku. Może on obliczyć stopy zwrotu kursu akcji ze wzoru
                                                           
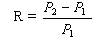
P2- bieżący kurs akcji, P1- poprzedni kurs akcji
Jeżeli mamy stopy zwrotu z poszczególnych okresów, to możemy policzyć średnią (oczekiwaną) stopę zwrotu oraz wariancję i odchylenie standardowe. Oczekiwana stopa zwrotu mierzy dochodowość akcji Bardzo Znanej Firmy, natomiast wariancja (lub odchylenie standardowe) mierzy ryzyko. Zatem Homo Oeconomicus grający na giełdzie wybiera między oczekiwaną stopą zwrotu oraz ryzykiem.

1. Załóżmy, że Homo Oeconomicus może zdeponować swoje pieniądze w banku (gdzie stopa zwrotu wynosi 5% a ryzyko- 0) lub kupić akcje ABC (oczekiwana stopa zwrotu- 3 %, odchylenie standardowe- 2 %). W tym przypadku inwestycja w akcje ABC nie ma sensu.
2. Teraz mamy akcje XYZ (oczekiwana stopa zwrotu- 10 %, odchylenie standardowe- 10 %). Ten wybór inwestycji jest racjonalny. Jednak istnieje duże ryzyko. Jeśli ktoś podejmuje duże ryzyko, to trzeba mu to wynagrodzić. W związku z tym należy zwiększyć dochodowość. Musi być relacja wymienna między ryzykiem a dochodowością.
3. Walor KLM (dochodowość- 7,5 %, odchylenie standardowe- 8 %). Ten wybór jest nieefektywny w porównaniu z depozytem bankowym.

Odchylenie standardowe jest lepszą miarą niż wariancja, gdyż wariancji nie można interpretować.
Można też zrobić rozkład empiryczny stóp zwrotu. Przy dużej liczbie obserwacji otrzymamy rozkład quasi-ciągły.
Jeśli mamy dwa rozkłady (A i B) o tej samej wartości oczekiwanej i narysujemy ich histogramy, to Homo Oeconomicus wybierze rozkład bardziej skupiony wokół wartości oczekiwanej.
W przypadku rozkładów o tym samym ryzyku, ale różnej wartości oczekiwanej, Homo Oeconomicus wybierze ten o większej wartości oczekiwanej. W tych dwóch przypadkach możemy dokonać wyboru bez znajomości funkcji użyteczności (stochastyczna dominacja). Wykorzystujemy tylko wnioskowanie statystyczne.

Jednak w tym przypadku nie ponosisz ryzyka, gdyż zawsze uda ci się sprzedać jakiś towar.
Przykład ten ilustruje to, że w celu zminimalizowania ryzyka najlepiej jest dobierać portfele o ujemnie skorelowanych walorach.