| |
|
TEORIA
PRODUKCJI
wprowadzenie
technologie produkcji
funkcja produkcji
Producent zawsze dąży do maksymalizacji zysków.

Koszty opisane są przez określoną funkcję kosztów, która zostanie omówiona
później.
Producent określa ilość produkcji, która zmaksymalizuje jego zysk. Natomiast
nie określa on jakości ani typu produktu. Zatem warunek maksymalizacji
zysku ma postać

Funkcja zysku może być różnie określona dla różnych warunków rynkowych
(doskonała konkurencja, mono-pol, oligopol). Producent działa na rynku
dóbr i usług (sprzedając swoje produkty) oraz na rynku czynników produkcji
(kupując czynniki produkcji).
Wielkość produkcji jest zależna od technologii oraz czynników produkcji.
Y = f(L, K, Z, KL, HK)
Technologia zmienia się w czasie. Postęp technologiczny umożliwia bardziej
efektywne wykorzystanie danych zasobów.
Czynniki produkcji:
- Praca,
- Kapitał (finansowy),
- Ziemia (grunt, na którym stoi fabryka, surowce naturalne),
- Kapitał ludzki (wiedza, umiejętności, know-how),
- Kapitał społeczny (dobre prawo, dobre instytucje).
Kapitał ludzki też może być inwestowany, jak również można inwestować
w ludzi. Kapitał ludzki jest akumulowany.
W mikroekonomii zajmujemy się na ogół tylko ziemią i kapitałem,
gdyż pozostałe czynniki są wielkościami niemierzalnymi.
Wynagrodzeniem pracy jest płaca (r), natomiast
wynagrodzeniem kapitału jest stopa procentowa (t). Stopa procentowa
jest kosztem utraconych
możliwości powstałych w wyniku nieulokowania kapitału w banku,
tylko przeznaczeniu go na inwestycje.
Możliwości wyboru technologii:
a. Kapitał i praca są doskonałymi substytutami.
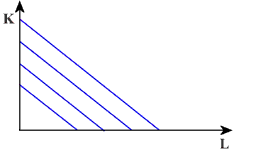
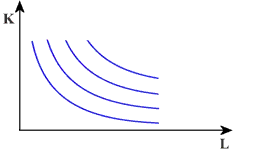
Daną wielkość produkcji można wyznaczyć za pomocą izokwanty (krzywej
jednakowego produktu). Izokwanta jest kombinacją różnych nakładów
pracy i kapitału potrzebnych do otrzymania określonej wielkości produkcji.
Relacja kapitału lub pracy do wielkości produkcji jest miarą efektywności
produkcji. W przypadku doskonałych substytutów niezależnie od wielkości
produkcji kapitał jest zastępowany pracą (lub odwrotnie) w stosunku
1 : 1 (pełna zastępowalność).
Relacja zastępowalności jednego czynnika
produkcji innym czynnikiem nazywana jest krańcową stopą technicznej
substytucji (MRTS). Zmiany nakładów pracy i kapitału przy jednoczesnym
zachowaniu tego samego poziomu produkcji można zapisać w następujący
sposób:

MPK - krańcowy produkt kapitału; MPL -
krańcowy produkt pracy
Po rozwiązaniu otrzymamy
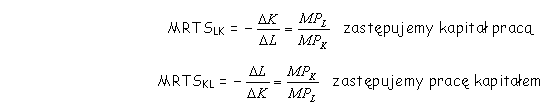
b. Praca i kapitał są doskonale komplementarne
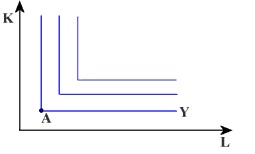
Doskonała komplementarność oznacza, że czynniki
produkcji muszą być używane zawsze w tych samych proporcjach.
Np.: Kierowca autobusu - praca i autobus - kapitał. Oba te czynniki
powinny być dobrane w proporcji 1 : 1 (punkt A). Izokwanta Y wyznacza
nakłady na obsługę jednej linii autobusowej w ciągu ośmiu godzin.
Gdyby zakupiono drugi autobus, to i tak można w danym momencie obsłużyć
tylko jeden autobus, chyba, że zostałby zatrudniony drugi kierowca.
Zatem dobieranie czynników w proporcjach innych niż ustalone wcale
nie powoduje wzrostu produkcji.
c. Funkcja Cobb Douglasa
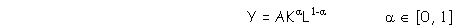
W przypadku tej funkcji kapitał i praca
mogą się wzajemnie zastępować. Proporcje, w jakich zastępuje się kapitał
i pracę zależą od proporcji
kapitału i pracy w stosunku do produkcji. MRTSLK będzie
coraz mniejsza. (Wyprowadzenie wzoru)
Funkcja produkcji
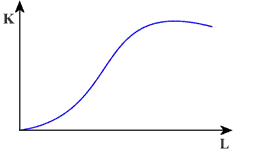
Niech będzie dana funkcja produkcji
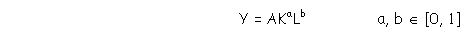
Przy szacowaniu funkcji produkcji ważna jest wielkość produkcji oraz
ilość czynników produkcji potrzebnych do wytworzenia określonej wielkości
produkcji. Należy też dokładnie określić dynamikę wzrostu produkcji.
Przy szacowaniu tego typu funkcji produkcji stosuje się ekonomikę skali
produkcji. Do pomiaru efektów skali produkcji wykorzystuje się parametry
a i b z funkcji produkcji.
Jeśli a + b > 1, to mamy rosnące efekty skali produkcji. Oznacza
to, że jeśli k-krotnie zwiększymy nakłady czynników produkcji,
to wielkość produkcji wzrośnie o więcej niż k-krotnie.
Np. Jeśli mamy funkcję produkcji postaci
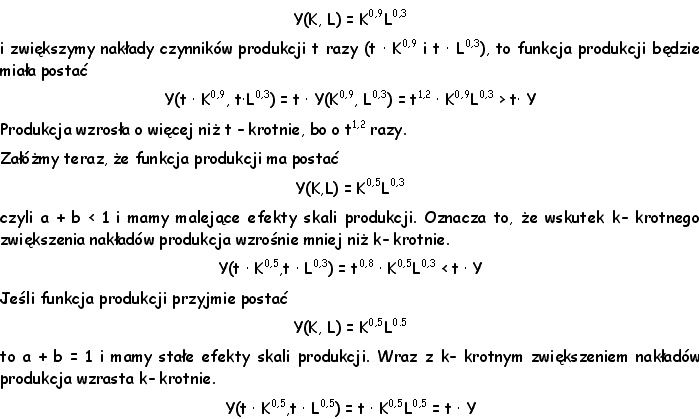
Ekonomika efektów skali dostarcza informacji o tym, czy opłaca się
łączyć lub dzielić firmy. W gospodarce występuje tendencja do znajdowania
optymalnej skali produkcji, tzn. rosnące efekty efekty skali są sygnałem
do łączenia firm, natomiast malejące efekty efekty skali informują
o konieczności dzielenia firm.
|
|
|